C Program To Implement Dictionary Using Hashing Songs
In this tutorial you will learn about Hashing in C and C with program example. You will also learn various concepts of hashing like hash table, hash function, etc. Hashing in Data StructureSearching is dominant operation on any data structure. Most of the cases for inserting, deleting, updating all operations required searching first.
So searching operation of particular data structure determines it’s time complexity. If we take any data structure the best time complexity for searching is O (log n) in AVL tree and sorted array only. Most of the cases it will take O (n) time. To solve this searching problem hashing concept introduced which will take O (1) time for searching. It’s constant time.
Hash Table and Hash FunctionEarlier when this concept introduced programmers used to create “Direct address table”. Direct address table means, when we have “n” number of unique keys we create an array of length “n” and insert element “i” at ith index of the array. That array is called Hash Table.
But due to this method even we have 10 elements of each range 1 lack, we should create table of size 1 lack for only 10 elements. Which is going to be waste of memory.To avoid this problem we fix the size of hash table (array) and map our elements into that table using a function, called Hash function. This function decides where to put a given element into that table. If we want to search also first apply hash function decide whether the element present in hash table or not.ExampleWe have numbers from 1 to 100 and hash table of size 10.
Hash function is mod 10. That means number 23 will be mapped to (23 mod 10 = 3) 3rd index of hash table.But problem is if elements (for example) 2, 12, 22, 32, elements need to be inserted then they try to insert at index 2 only. This problem is called Collision. To solve this collision problem we use different types of hash function techniques. Those are given below. Chaining.
Open addressing. Linear probing. Quadratic probing.
By using that key you can access the element in O(1) time. Using the key, the algorithm (hash function) computes an index that suggests where an entry can be found or inserted. Hashing is implemented in two steps: An element is converted into an integer by using a hash function. This element can be used as an index to. Oct 05, 2016 The separate chaining hash table implementation makes use of Linked List in C Programming. There are different hashing algorithms such as Bucket Hashing, Linear Probing, Separate Chaining, etc. Hash tables offers finding the element in less key comparisons, making the search operation to execute in a Constant Time.
Double hashingThese also called collision resolution techniques. ChainingIn hash table instead of putting one element in index we maintain a linked list. When collision happened we place that element in corresponding linked list. Here some space is wasted because of pointers.Open AddressingIn case if we have collision we again calculate the hash value using corresponding hash function.
But this time we do some minor modifications to that input. This process of searching for empty space to insert element in called Probing.Probing hash function is: h (k, i)here k is the key value which is to be inserted. And i is number of collision with that element.Example: If we are inserting 2, we find its hash value using h (2, 0) because it’s first collision. Suppose the answer (index) to this function index already occupied we again need to apply h (2, 1) to hash function.Linear ProbingLet hash function is h, hash table contains 0 to n-1 slots.Now we want to insert an element k. If it results “x” and the index “x” already contain a value then we again apply hash function that h (k, 1) this equals to (h (k) + 1) mod n.General form: h1 (k, j) = (h (k) + j) mod nExample: Let hash table of size 5 which has function is mod 5 has already filled at positions 0, 2, 3.Now new element 10 will try to insert. 10 mod 5 = 0.
But index 0 already occupied. So it checks (probes) next (index 1) position.
So 10 will insert at index 1.Now element 11 will try to insert. 11 mod 5 = 1. But index 1 already occupied, check index 2 it also occupied (data given), 3 also occupied. So it will insert at index 4 which is empty.We can observe that it linearly checking for next empty position.
So it’s called linear probing.Problems with linear probing:. Primary clustering: There is a chance that continuous cells occupied, then the probability of new element insertion will get reduced. This problem is called primary clustering.
C Program To Implement Dictionary Using Hashing Songs In English
Secondary clustering: If two elements get same value at first hash function, they follow same probe sequence.Quadratic ProbingIt is same as linear probing. But when collision occurs we use different function. If collision happened that element try to occupy at quadratic distance instead of linear distance.Due to this “Primary clustering” will be reduced. But secondary clustering won’t be eliminated.Double HashingHere we use two hash functions.h1 (k) = (h1 (k) + i h2 (k)) mod n.
Here h1 and h2 are two hash functions.Here the next prob position will depend on two functions h1 and h2 also.Advantages by this method are there is no chance of primary clustering. And also Secondary clustering also eliminated. Facebreak facebook brute force programming. Chaining vs Open Addressing ChainingOpen AddressingElements can be stored at outside of the tableIn open addressing elements should be stored inside the table onlyIn chaining at any time the number of elements in the hash table may greater than the size of the hash tableIn open addressing the number of elements present in the hash table will not exceed to number of indices in hash table.In case of deletion chaining is the best methodIf deletion is not required. Only inserting and searching is required open addressing is betterChaining requires more spaceOpen addressing requires less space than chaining.Program for Hashing in CBelow is the implementation of hashing or hash table in C.

When I did this, I used the hash table for symbols, not for entities.For each symbol, I had a list of entities. Each entity was in twolists, one from the symbol, and the second from the scope. The listfrom the symbol was managed like a stack: when I accessed a symbol, theentity in scope was always the first in the list. When I left a scope,I walked its list of entities, and removed them from the list ofsymbols.This was some time ago, before the STL (and even before C); Iimplemented everything by hand, and used invasive chaining for thelists, with the algorithm so designed that I could remove an elementfrom a list without knowing where the list itself was. (This isrelatively easy with hand written double linked lists.) Today, with theSTL (and with the importance of locality of access), I'd probably simplyput a pointer to the head of the list in each entity. With the STL, andconsiderations of locality, I'd probably use std::vector for the listfor each entity (the symbol table thus being a map of std::string tostd::vector).
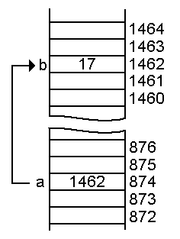
Symbol table lookup, once the entry is found, is simplycalling back on the vector (after checking that it isn't empty, ifyou don't purge the entry when the vector becomes empty). When youcreate new entity, in a new scope, you call pushback on the vector,and save the address of the vector in an entry for the scope (astd::stack of std::vector.); when leavingscope, you iterate over the vector at the top of this stack, callingpopback on all of its entries, then pop it off the stack.
Dictionary
(Andobviously, when entering a new scope, you push a new empty vector ontothe scope stack.)Maintaining the double list means that for all operations, you knowexactly which element to access, without having to iterate overanything; there's never any access to an entity to see if it's the oneyou're looking for. In my day, it was fairly straightforward, but a lotof code, requiring considerable care, and my implemention probablywouldn't be that fast today, because of poor locality. Today, with theSTL, you need a lot less code, and by using std::vector for all of thelists, you get slightly better locality; you still have to be careful,so that you don't end up saving iterators which will be invalidated.(But implemented as described above, you shouldn't need to; all accessesare always to the last element of the vector, so saving the address ofthe vector itself is sufficient. Provided, of course, that your hashimplementation doesn't move the vectors.).